you’re just a tutor and not actually a teacher?
Both - see the problem with the logic you use?
Let me know when you decide to consult a textbook about this.
💡𝚂𝗆𝖺𝗋𝗍𝗆𝖺𝗇 𝙰𝗉𝗉𝗌📱
- 0 Posts
- 92 Comments
Joined 1 year ago
Cake day: November 25th, 2023
You are not logged in. If you use a Fediverse account that is able to follow users, you can follow this user.
a single sentence of a wikipedia article without me handfeeding it to you
And I told you why it was wrong, which is why I read Maths textbooks and not wikipedia.
I’m sorry for your students
My students are doing good thanks
The notation is not intrinsically clear
It is to me, I actually teach how to write it.
Exactly! It’s in math textbooks, in both ways!
And both ways are explained, so not ambiguous which is which.
Ummm, I was agreeing with you??
Anyways, I’m a Maths teacher who has taught this topic many times - what would I know?
multiple always happens first. But apparently it’s what’s left side first
Multiplication and division are equal precedence (and done left to right) if that’s what you’re talking about, but the issue is that a(b+c) isn’t “multiplication” at all, it’s a bracketed term with a coefficient which is therefore subject to The Distributive Law, and is solved as part of solving Brackets, which is always first. Multiplication refers literally to multiplication signs, of which there are none in the original question. A Term is a product, which is the result of a multiplication, not something which is to be multiplied.
If a=2 and b=3, then…
axb=2x3 - 2 terms
ab=6 - 1 term
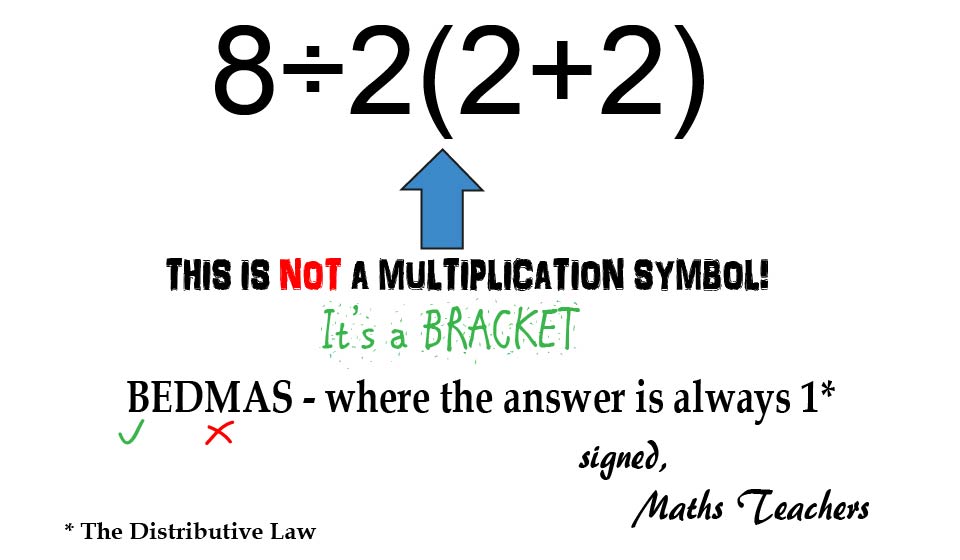
You can define your notation that way if you like
Nothing to do with me - it’s in Maths textbooks.
without knowing the conventions the author uses, it’s ambiguous
Well they should all be following the rules of Maths, without needing to have that stated.
which clearly states that the distributive property is a generalization of the distributive law
Let me say again, people calling a Koala a Koala bear doesn’t mean it actually is a bear. Stop reading wikipedia and pick up a Maths textbook.
You seem to be under the impression that the distributive law and distributive property are completely different statements
It’s not an impression, it’s in Year 7 Maths textbooks.
this certainly is not 7th year material
And yet it appears in every Year 7 textbook I’ve ever seen.
Looks like we’re done here.
If you read the wikipedia article
…which isn’t a Maths textbook!
also stating the distributive law, literally in the first sentence
Except what it states is the Distributive property, not The Distributive Law. If I call a Koala a Koala Bear, that doesn’t mean it’s a bear - it just means I used the wrong name. And again, not a Maths textbook - whoever wrote that demonstrably doesn’t know the difference between the property and the law.
This is something you learn in elementary school
No it isn’t. This is a year 7 topic. In Primary School they are only given bracketed terms without a coefficient (thus don’t need to know The Distributive Law).
be assured that I am sufficiently qualified
No, I’m not assured of that when you’re quoting wikipedia instead of Maths textbooks, and don’t know the difference between The Distributive Property and The Distributive Law, nor know which grade this is taught to.
Wikipedia is not intrinsically less accurate than maths textbooks
BWAHAHAHAHA! You know how many wrong things I’ve seen in there? And I’m not even talking about Maths! Ever heard of edit wars? Whatever ends up on the page is whatever the admin believes. Wikipedia is “like an encyclopedia” in the same way that Madonna is like a virgin.
but you are misunderstanding them
And yet you have failed to point out how/why/where. In all of your comments here, you haven’t even addressed The Distributive Law at all.
Whether you write it as a(b+c) = ab + ac or as a*(b+c) = ab + ac is insubstantial
And neither of those examples is about The Distributive Law - they are both to do with The Distributive Property (and you wrote the first one wrong anyway - it’s a(b+c)=(ab+ac). Premature removal of brackets is how many people end up with the wrong answer).
If I write f^{-1}(x), without context, you have literally no way of knowing whether I am talking about a multiplicative or a functional inverse, which means that it is ambiguous
The inverse of the function is f(x)^-1. i.e. the negative exponent applies to the whole function, not just the x (since f(x) is a single term).
P.S. feel free to read through and use my thread on order of operations.
inside radicals
I had to look up what that meant (should’ve done that the first time - sorry) - have never heard that before, must be a local terminology.
So, square roots (or other roots) can be expressed as an exponent - e.g. the square root of 2 is the same as 2 to the power ½ - so that’s covered by “E”, exponents! (or I for Index, or O for to the Order of, depending on your area)
I appreciate your mention of the importance of teaching the difference between operators and terms
Thank you.
My pedagogical background is in the sciences and I’m much better at doing math than teaching it
Oh god, welcome to why I have so many people argue with me, a Maths teacher, about it. There’s a whole bunch of Youtubes and blogs out there by Physics majors. I’m like “OMG, why are you trusting someone with a Physics major over someone with a Maths major - god help me”.
I would like if math classes (in my area) did more explicitly teach the difference between terms and operators
So what area are you in? A country will do. You said PEMDAS so I’m guessing the U.S.? I’ve heard via Youtubes/blogs that indeed there is more confusion with what is taught there, but I ended up Googling for U.S. textbooks, and found the same thing being taught in the textbook, so I’m not sure where this “that’s not what they teach in the U.S.” is coming from (why I was Googling for U.S. textbooks in the first place). Is the standard of teachers there actually worse than elsewhere? Or is it perhaps (possibly more likely) that there’s just more U.S. people posting, therefore more people who’ve forgotten the actual rules, and are just (as I’ve seen many times) they’re just blaming it on what they were taught (which I’ve usually found isn’t true at all).
Ok, that’s a start. In your simple example they are all equal, but they aren’t all the same.
yn+y - 2 terms
y(n+1) - 1 term
y×(n +1) - 2 terms
To see the difference, now precede it with a division, like in the original question…
1÷yn+y=(1/yn)+y
1÷y(n+1)=1/(yn+y)
1÷y×(n +1)=(n +1)/y
Note that in the last one, compared to the second one, the (n+1) is now in the numerator instead of in the denominator. Welcome to why having the (2+2) in the numerator gives the wrong answer.
Do you not understand that syntax is its own set of rules?
Yes, the rules of Maths, as I was already saying. I’m a Maths teacher. I take it you didn’t read the link then.
Please learn some math
I’m a Maths teacher - how about you?
Quoting yourself as a source
I wasn’t. I quoted Maths textbooks, and if you read further you’ll find I also quoted historical Maths documents, as well as showed some proofs.
I didn’t say the distributive property, I said The Distributive Law. The Distributive Law isn’t ax(b+c)=ab+ac (2 terms), it’s a(b+c)=(ab+ac) (1 term), but inaccuracies are to be expected, given that’s a wikipedia article and not a Maths textbook.
I did read the answers, try doing that yourself
I see people explaining how it’s not ambiguous. Other people continuing to insist it is ambiguous doesn’t mean it is.
The y(n+1) is same as yn + y
No, it’s the same as (yn+y). You can’t remove brackets unless there is only 1 term left inside.
if you removed the “6÷” part. It’s
…The Distributive Law.
That just states that a*(b + c) = ab + ac
No, The Distributive Law states that a(b+c)=(ab+ac), and that you must expand before you simplify.
For some simple exanples,
Examples by people who simply don’t remember all the rules of Maths. Did you read the answers?
If they weren’t ambiguous, then you wouldn’t see them getting popular
#MathsIsNeverAmbiguous They get popular because people who don’t remember all the rules of Maths want to argue with the people who do remember all the rules of Maths. #DontForgetDistribution
different systems of infix notation
There’s not different rules of Maths though, and the people “debating” the answer are those who don’t remember all the rules.
Yeah, right answer but wrong reason. There’s no such thing as implicit multiplication.
Correct, and that’s because of Terms - 8÷2(2+2) is 2 terms, with the (2+2) in the denominator, but 8÷2×(2+2) is 3 terms, with the (2+2) in the numerator… hence why people get the wrong answer when they add an extra multiply in.
Right, because it’s not “multiplication” at all (only applies literally to multiplication signs), it’s a coefficient of a bracketed term, which means we have to apply The Distributive Law as part of solving Brackets.
Yeah, the actual rule is Left associativity, and going left to right is the easy way to obey that.