I wrote a (very long) blog post about those viral math problems and am looking for feedback, especially from people who are not convinced that the problem is ambiguous.
It’s about a 30min read so thank you in advance if you really take the time to read it, but I think it’s worth it if you joined such discussions in the past, but I’m probably biased because I wrote it :)
I am so glad that nothing I do in life will ever cause this problem to matter to me.
The way I was taught in school, the answer is clearly 1, but I did read the blog post and I understand why that’s actually ambiguous.
Fortunately, I don’t have to care, so will sleep well knowing the answer is 1, and that I’m as correct as anyone else. :-p
why that’s actually ambiguous.
It isn’t actually ambiguous. You have remembered what you were taught in school, unlike the author of the blog post, who manages to write the whole thing without ever once checking a Maths textbook (which would reveal the only correct answer to be 1).
I think this speaks to why I have a total of 5 years of college and no degree.
Starting at about 7th grade, math class is taught to every single American school child as if they’re going to grow up to become mathematicians. Formal definitions, proofs, long sets of rules for how you manipulate squiggles to become other squiggles that you’re supposed to obey because that’s what the book says.
Early my 7th grade year, my teacher wrote a long string of numbers and operators on the board, something like 6 + 4 - 7 * 8 + 3 / 9. Then told us to work this problem and then say what we came up with. This divided us into two groups: Those who hadn’t learned Order of Operations on our own time who did (six plus four is ten, minus seven is three, times eight is 24, plus three is 27, divided by nine is three) Three, and who were then told we were wrong and stupid, and those who somehow had, who did (seven times eight is 56, three divided by nine is some tiny fraction…) got a very different number, and were told they were right. Terrible method of teaching, because it alienates the students who need to do the learning right off the bat. And this basically set the tone until I dropped out of college for the second time.
Yes, unfortunately there are some bad teachers around. I vividly remember the one I had in Year 10, who literally didn’t care if we did well or not. I got sick for an extended period that year, and got a tutor - my Maths improved when I had the tutor (someone who actually helped me to learn the material)!
What the heck are you all fighting about? It’s BODMAS.
They’re arguing about whether Distribution is Multiplication or not. Spoiler alert: it isn’t, it’s Brackets.
PEDMAS sounds like one of those cheap, off-brand protein powders that are abused by body-builders.
So what does BODMAS sound like to the other side?
samdob
I disagree. Without explicit direction on OOO we have to follow the operators in order.
The parentheses go first. 1+2=3
Then we have 6 ÷2 ×3
Without parentheses around (2×3) we can’t do that first. So OOO would be left to right. 9.
In other words, as an engineer with half a PhD, I don’t buy strong juxtaposition. That sounds more like laziness than math.
How are people upvoting you for refusing to read the article?
Because as a high school Maths teacher as soon as I saw the assertion that it was ambiguous I knew the article was wrong. From there I scanned to see if there were any Maths textbooks at any point, and there wasn’t. Just another wrong article.
Lol. Read it.
Why would I read something that I know is wrong? #MathsIsNeverAmbiguous
Mathematical notation however can be. Because it’s conventions as long as it’s not defined on the same page.
Mathematical notation however can be.
Nope. Different regions use different symbols, but within those regions everyone knows what each symbol is, and none of those symbols are in this question anyway.
Because it’s conventions as long as it’s not defined on the same page
The rules can be found in any high school Maths textbook.
Let’s do a little plausibility analysis, shall we? First, we have humans, you know, famously unable to agree on an universal standard for anything. Then we have me, who has written a PhD thesis for which he has read quite some papers about math and computational biology. Then we have an article that talks about the topic at hand, but that you for some unscientific and completely ridiculous reason refuse to read.
Let me just tell you one last time: you’re wrong, you should know that it’s possible that you’re wrong, and not reading a thing because it could convince you is peak ignorance.
I’m done here, have a good one, and try not to ruin your students too hard.
Interesting, I didn’t know about strong implicit multiplication. So I would have said the result is 9. All along my studies in France, up to my physics courses at University, all my teachers used weak implicit multiplication. Could be it’s the norm in France, or they only use it in math studies at University.
I didn’t know until now that I unconsciously use strong implicit multiplication (meaning that I get the answer “1”). I believe it happens more or less as a consequence of starting inside the parentheses and then working my way out.
It is a funny little bit of notational ambiguity, so it is funny that people get riled up about it.
It is a funny little bit of notational ambiguity
It’s not ambiguous - it’s The Distributive Law. You got the correct answer, you just forgot what the rule is called (as opposed to people who forget the rule altogether).
In a scientific context it’s actually very rare to run into that issue because divisions are mostly written as fractions which will completely mitigate the issue.
The strong implicit multiplication will only cause ambiguity after a division with inline notation. Once you use fractions the ambiguity vanishes.
In practice you also rarely see implicit multiplications between numbers but mostly between variables or variables and their coefficients.
Def not a math major (BS/PharmD), but your explanation was like seeing through a visual illusion for the first time! lol
I was always taught PEMDAS growing up, and that the MD and the AS was read left to right in an equation like above. But stating the division as a fraction completely changes my mind now about how this calculation works. I think what would happen in a calculation I use every day if the former was used.
Example: Cockcroft-Gault Equation (estimation of renal function)
(140-age)(kg) / 72(SCr) vs (140-age) X kg ➗72 X SCr
In the first eq (correct one) an 80yo patient who weighs 65kg and has an SCr ~ 1.5 = 36.11
In the latter it = 81.25 (waaay too high for an 80yo lol)
edit: calculation variable
But stating the division as a fraction completely changes my mind now about how this calculation works
But division and fraction aren’t the same thing - the former separates terms, the latter is a single term.
(140-age)(kg) / 72(SCr) vs (140-age) X kg ➗72 X SCr
The different answers for these two isn’t because of / vs ➗, but because in the second one you have added extra multiplications in, thus breaking up some of the terms, and SCr has consequently been flipped from being in the denominator to being in the numerator. i.e. AK/72Scr vs. AK/72xSCr.
Yes of course, we always used fractions so there was no ambiguity. Last time I saw the division symbol must have been in primary school!
You would’ve done dividing by fractions in high school, which requires both. Fractions and division aren’t the same thing.
I recall learning in school that it should be left to right when in doubt. Probably a cop-out from the teacher
“when in doubt” is a bit broad but left to right is a great default for operations with the same priority. There is actually a way to calculate in any order if divisions are converted to multiplications (by using the reciprocal value) and subtractions are converted to additions (by negating the value) that requires at least a little bit of math knowledge and experience so it’s typically not taught until later to prevent even more confusion.
For example this: 6 / 2 * 3 can also be rewritten as 6 * 2⁻¹ * 3 and because multiplication is commutative you can now do it in any order for example like 3 * 6 * 2⁻¹
You can also “rearrange” the order without changing the meaning if you move the correct operation (left to the number) with it (should only be done with explicit multiplication)
6 / 2 * 3 into 6 * 3 / 2 (note that I moved the division with the 2)
You can even bring the two to the front. Just remember that left to the six is an “imaginary” (don’t quote me ^^) multiplication. And because we can’t just move “/2” to the beginning we have to insert a one (empty product - check Wikipedia) like so:
1 / 2 * 6 * 3
This also works for addition and subtraction
7 + 8 - 5
You can move them around if you take the operation left to the number with it. With addition the “imaginary” operation at the beginning is a plus sign and the implicit number you use is zero (empty sum - check Wikipedia)
8 - 5 + 7
or like this
0 - 5 + 8 + 7
because with negative numbers you can use the minus sign to indicate negative numbers you can even drop the leading zero like this
-5 + 8 + 7
That’s not really possible with multiplication because “/2” is not a valid notation for “1/2”
6 / 2 * 3
Semi-related: something in me wants to read that as 6 / (2*3), because 6 * 3 / 2 feels like a much more ‘natural’ way to write it
Semi-related: something in me wants to read that as 6 / (2*3)
100% related actually, since that’s the actual next line of working out. i.e. you cannot remove brackets unless there is only 1 term left inside, a mistake which those who have prematurely removed brackets have made and ended up with the wrong answer (because it flips the 3 from being in the denominator to being in the numerator).
6 / 2 * 3 into 6 * 3 / 2 (note that I moved the division with the 2)
And note that it doesn’t work if the multiply was an addition. e.g. 6/2+3=6 but 6+3/2=7.5. Multiplication and division are both binary operators, and you can’t move them around unless you also move the term to the left with it. i.e. 6/2+3=6. 3+6/2=6.
Just remember that left to the six is an “imaginary” (don’t quote me ^^) multiplication
No, to the left of the 6 is an actual plus sign, but we don’t write plus signs if it’s at the start of an expression. +6 and x6 aren’t the same thing at all (and, since x is a binary operator, you couldn’t write just x6 anyway - there would have to be a term to it’s left). No expression ever starts with x6.
That’s not really possible with multiplication because “/2” is not a valid notation for “1/2”
It’s not a valid notation for multiplication either - both multiplication and division are binary operators and must be written with 2 terms.
Having read your article, I contend it should be:
P(arentheses)
E(xponents)
M(ultiplication)D(ivision)
A(ddition)S(ubtraction)
and strong juxtaposition should be thrown out the window.Why? Well, to be clear, I would prefer one of them die so we can get past this argument that pops up every few years so weak or strong doesn’t matter much to me, and I think weak juxtaposition is more easily taught and more easily supported by PEMDAS. I’m not saying it receives direct support, but rather the lack of instruction has us fall back on what we know as an overarching rule (multiplication and division are equal). Strong juxtaposition has an additional ruling to PEMDAS that specifies this specific case, whereas weak juxtaposition doesn’t need an additional ruling (and I would argue anyone who says otherwise isn’t logically extrapolating from the PEMDAS ruleset). I don’t think the sides are as equal as people pose.
To note, yes, PEMDAS is a teaching tool and yes there are obviously other ways of thinking of math. But do those matter? The mathematical system we currently use will work for any usecase it does currently regardless of the juxtaposition we pick, brackets/parentheses (as well as better ordering of operations when writing them down) can pick up any slack. Weak juxtaposition provides better benefits because it has less rules (and is thusly simpler).
But again, I really don’t care. Just let one die. Kill it, if you have to.
Division comes before Multiplication, doesn’t it? I know BODMAS.
This actually explains alot. Murica is Pemdas but Canadian used Bodmas so multiply is first in America.
As far as I understand it, they’re given equal weight in the order of operations, it’s just whichever you hit first left to right.
Yeah 100% was not taught that. Follow the pemdas or fail the test. Division is after Multiply in pemdas.
I put the equation into excel and get 9 which only makes sense in bodmas.
It doesn’t make sense in BODMAS either. Expanding Brackets has precedence of… Brackets, not “multiplication” - “Multiplication” refers literally to multiplication signs, of which there are none in this question.
The y(n+1) is same as yn + y if you removed the “6÷” part. It’s implied multiplication.
The y(n+1) is same as yn + y
No, it’s the same as (yn+y). You can’t remove brackets unless there is only 1 term left inside.
if you removed the “6÷” part. It’s
…The Distributive Law.
What’s especially wild to me is that even the position of “it’s ambiguous” gets almost as much pushback as trying to argue that one of them is universally correct.
Last time this came up it was my position that it was ambiguous and needed clarification and had someone accuse me of taking a prescriptive stance and imposing rules contrary to how things were actually being done. How asking a person what they mean or seeking clarification could possibly be prescriptive is beyond me.
Bonus points, the guy telling me I was being prescriptive was arguing vehemently that implicit multiplication having precedence was correct and to do otherwise was wrong, full stop.
Without any additional parentheses, the division sign is assumed to separate numerators and denominators within a complete expression, in which case you would reduce each separately. It’s very, very marginally ambiguous at best.
You are correct with your definition - Terms are separated by operators and joined by grouping symbols - and it’s consequently not ambiguous at all (using so-called “weak juxtaposition” breaks that rule).
Assumed by whom? Clearly not everyone.
It’s what is actually taught in high school, so there are those who remember and those who don’t.
What’s especially wild to me is that even the position of “it’s ambiguous” gets almost as much pushback as trying to argue that one of them is universally correct.
That’s because following the rules of Maths is universally correct.
arguing vehemently that implicit multiplication having precedence was correct and to do otherwise was wrong, full stop
He was using the wrong words, but he was correct - the actual rules are The Distributive Law and Terms (“implicit multiplication” is a rule made up by those who have forgotten these 2 rules).
When I went to college, I was given a reverse Polish notation calculator. I think there is some (albeit small) advantage of becoming fluent in both PEMDAS and RPN to see the arbitrariness. This kind of arguement is like trying to argue linguistics in a single language.
Btw, I’m not claiming that RPN has any bearing on the meme at hand. Just that there are different standards.
This comment is left by the HP50g crew.
It would be better if we just taught math with prefix or postfix notation, as it removes the ambiguity.
There isn’t ambiguity to begin with - just people who have forgotten the rules of Maths.
Ambiguity is fine. It would tedious to the point of distraction to enforce writing math without ambiguity. You make note of conventions and you are meant to realize that is just a convention. I’m amazed at the people who are planting their feet to fight for something that what they were taught in third grade as if the world stopped there.
You’re right though. We should definitely teach different conventions. But then what would facebook do for engagement?
enforce writing math without ambiguity
It already is written without ambiguity.
were taught in third grade
This is actually taught in Year 7 - the people who only remember the 3rd Grade version of the rules are the ones getting it wrong.
👍 That was actually one of the reasons why I wrote this blog post. I wanted to compile a list of points that show as clear as humanity possible that there is no consensus here, even amongst experts.
That probably won’t convince everybody but if that won’t probably nothing will.
I wanted to compile a list of points that show as clear as humanity possible that there is no consensus here, even amongst experts
And I wrote a bunch of fact checks pointing out there is consensus amongst the actual experts - high school Maths teachers and textbook authors, the 2 groups who you completely ignored in your blog post.
It’s not ambiguous, it’s just that correctly parsing the expression requires more precise application of the order of operations than is typical. It’s unclear, sure. Implicit multiplication having higher precedence is intuitive, sure, but not part of the standard as-written order of operations.
I’d really like to know if and how your view on that matter would change once you read the full post. I know it’s very long and a lot of people won’t read it because they “already know” the answer but I’m pretty sure it would shift your perception at least a bit if you find the time to read it.
My opinion hasn’t changed. The standard order of operations is as well defined as a notational convention can be. It’s not necessarily followed strictly in practice, but it’s easier to view such examples as normal deviation from the rules instead of an implicit disagreement about the rules themselves. For example, I know how to “properly” capitalize my sentences too, and I intentionally do it “wrong” all the time. To an outsider claiming my capitalization is incorrect, I don’t say “I am using a different standard,” I just say “Yes, I know, I don’t care.” This is simpler because it accepts the common knowledge of the “normal” rules and communicates a specific intent to deviate. The alternative is to try to invent a new set of ad hoc rules that justify my side, and explain why these rules are equally valid to the ones we both know and understand.
The difference is that there are two sets of rules already in use by large groups of people, so which do you consider correct?
There’s only 1 set of rules, and 2 sets of people - those who follow the rules and those who don’t.
There aren’t.
They weren’t asking you if there are two sets of rules, we’re in a thread that’s basically all qbout the Weak vs. Strong juxtaposition debate, they asked you which you consider correct.
Giving the answer to a question they didn’t ask to avoid the one they did is immature.
My TI-84 Plus is my holy oracle, I will go with whatever it says.
And then get distracted and play some Doom.
TI calcs give the wrong answer, and it’s in their manual why - they only follow the Primary School rule (“inside the brackets”), not the High School rule which supersedes it (The Distributive Law).
It will give 9, just like my 89 emulator. It treats division like a fraction. For a TI, the entire denominator of a fraction needs to be in parentheses or you get into trouble.
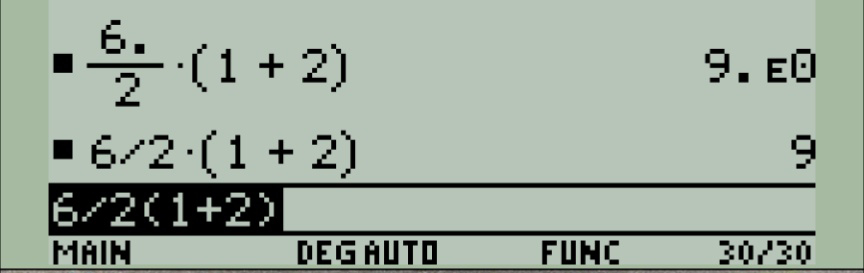
It treats division like a fraction
Which is why it gives the wrong answer.
Also you shouldn’t be adding a dot between the 2 and the brackets - that also changes the answer.
Typo in article:
If you are however willing to except the possibility that you are wrong.
Except should be ‘accept’.
Not trying to be annoying, but I know people will often find that as a reason to disregard academic arguments.
academic arguments
The “academic arguments” can be ignored since this is actually high school Maths - it’s taught in Year 7-8.
A person not knowing the difference in usage between except and accept sounds like a perfectly reasonable reason to disregard their math skills.
Especially when said person keeps making incorrect statements about Maths and ignores completely what is taught in high school.
I feel like if a blog post presents 2 options and labels one as the “scientific” one… And it is a deserved Label. Then there is probably a easy case to be made that we should teach children how to understand scientific papers and solve the equation in it themselves.
Honestly I feel like it reads better too but that is just me
We do teach children how to solve this. It’s not children who get it wrong - it’s adults that get it wrong! Cos they’ve forgotten the rules of Maths (in this case The Distributive Law and Terms).
I’m not sure if I’d call it the “scientific” one. I’d actually say that the weak juxtaposition is just the simple one schools use because they don’t want to confuse everyone. Scientist actually use both and make sure to prevent ambiguity. IMHO the main takeaway is that there is no consensus and one has to be careful to not write ambiguous expressions.
I mean the blog post says
“If you are a student at university, a scientist, engineer, or mathematician you should really try to ask the original author what they meant because strong juxtaposition is pretty common in academic circles, especially if variables are involved like in $a/bc$ instead of numbers.”
It doesn’t say scientific but…
I’m a scientist and I’ve only ever encountered strong juxtaposition in quick scribbles where everyone knows the equation already. Normally we’re very careful to use fraction notation (or parentheses) when there’s any possibility of ambiguity. I read the equation and was shocked that anyone would get an answer other than 9.
I read the equation and was shocked that anyone would get an answer other than 9
As a Maths teacher, I’m shocked whenever anyone ever gets an answer other than 1. I’m not sure how you came up with 9 when you previously said you’ve only ever seen strong juxtaposition? You can only get 9 with so-called “weak juxtaposition” (which is wrong).
My comment was directed to the blog post and the claims contained in it.
The blog post claims it is popular in academy, if that is a deserved label, then I don’t understand how the author of the post lands on “there is no good or bad way, they are all valid”. I am in favor of strong juxtaposition but that is not the case that I am making here. Sorry for the confusion.
The blog post claims it is popular in academy
The blog post also completely ignores what is actually taught in high school - as found in Year 7-8 Maths textbooks - which indicates how much credibility you should attach to the blog post - none.
So I shouldn’t use text written by the author to understand the pov of the author and critic his pov because it is “only” a blog post, noted.
Not sure how you came up with that conclusion. I never said anything about it being “just a blog post”.
You said…
I don’t understand how the author of the post lands on “there is no good or bad way, they are all valid”
And I’m pointing out he arrived at that by ignoring what’s taught in high school, which is where it’s taught (not in academia). It’s like saying “It’s ambiguous if there’s such a thing as rain” if you present weather evidence which has omitted every single rainy day that has happened. i.e. cherry-picking. Every single blog which says it’s ambiguous has done the exact same thing. You can find what actually is taught in high school here
I’d actually say that the weak juxtaposition is just the simple one schools use
Schools don’t teach “weak juxtaposition” - they teach the actual rules of Maths! As per what’s in Maths textbooks. It’s adults who’ve forgotten the rules who make up the “weak juxtaposition” rule. See Lennes.
Build two cases, calculate for both, drag both case through the entirety of both problems, get two answers, make a case for both answers, end up with two hypothesis. Easy!
Check a high school Maths textbook - even easier!
Who gives a shit about order of operations. In a real world scenario you’ll know what to do
Unfortunately, demonstrably, a lot of people don’t know what to do.
It’s not ambiguos nor an communication problem, it’s basic Math



And WolframAlpha did division before brackets (turned 6/2 into a fraction, thus making it a single term instead of separate terms, all before doing brackets), thus violating the order of operations rules.
You should read the part about WolframAlpha in the blog.
https://www.wolframalpha.com/input?i=6%2Fxy+where+x%3D2%2C+y%3D3
Both of those screenshots, the input is a fraction, thereby removing the ambiguity. But when you use the division symbol, an ambiguity arises. This is why you should never, for any reason, use a division symbol.
Division doesn’t mean fraction. Division is 2 terms, a fraction is 1 term. Terms are separated by operators and joined by grouping symbols. If you change the division to a fraction you change the number of terms and change the answer (and you also would’ve just done division before brackets, which violates the order of operations rules).
…he literally used the
÷operator in the top screenshot. WolframAlpha interprets it as synonymous with/.When putting in ambiguous inputs to WolframAlpha, it does its best to interpret it so that it’s can give an answer, and it shows you underneath how it interpreted it. That doesn’t mean there wasn’t any ambiguity to begin with.
Right. I’m saying both / and ÷ are ambiguous in that context. WA interprets both symbols as having equivalent meaning.
WA interprets both symbols as having equivalent meaning
The wrong meaning. It interprets them both as a fraction bar, thus giving the wrong answer.